Epilogue - there is more than one way

I hope you had fun with the game, just like I do, the answer provided here are meant to be a sample solution. There are, of course, other ways to accomplish the same goal. I am sure the answers are correct, but in case you think my answer is inaccurate or you have better solutions, please leave me comments!

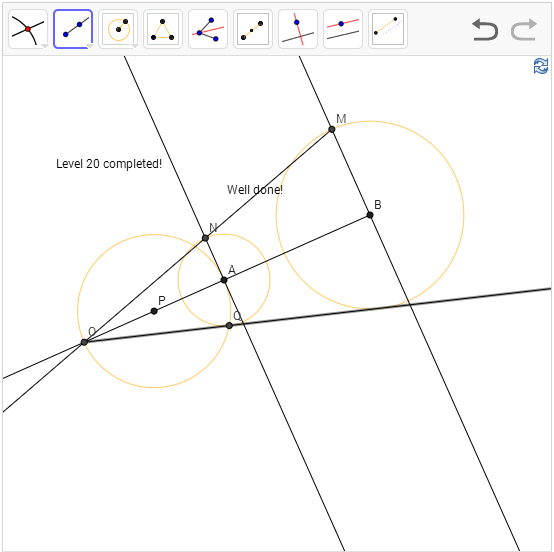
Level 20: Construct a line (segment) tangent to both circles. Construct the outer tangent line.

Hint: Think ratios.

Solution: First construct the ray AB, and let the outer tangent line intersect AB at O. Now OA:OB should be (radius of A: radius of B). To find such point O, we use the similar triangle NAO and MBO. Once we found the point O, we need to find a point C on circle A such that OCA is a right angle. Now we leverage another fact, angle subtended by the diameter on a circle is the right angle, so we construct the midpoint P of O and A, draw the circle with center P and radius PA, so the intersection between the circle would give us the point C and we are done.

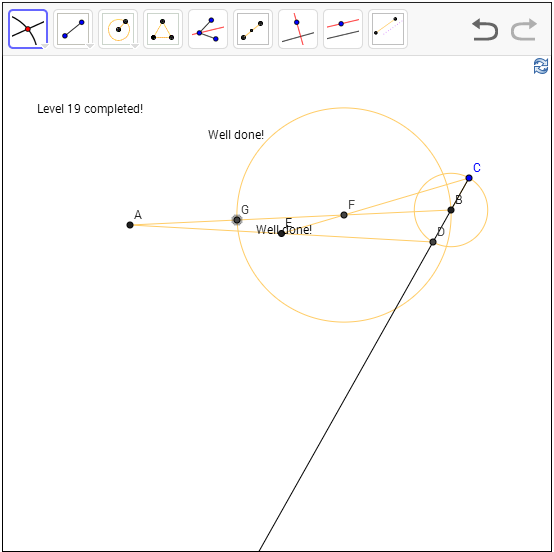
Level 19: Construct two points, such that the segment is cut into three equal pieces.

Hint: Perhaps unrelated – study the centroid of a triangle.

Solution: The centroid of a triangle is found by intersecting the median, the median is defined by the intersection between the midpoint of an edge and the opposite vertex. The interesting thing about this is that it can be shown that the intersection point always cut the median into two-third on the vertex side and one third on the remaining side. It is this property that we will leverage for this level.

With that in mind, we make AB the median, which means A is the opposite vertex and B is the midpoint of some base line, construct the base line by creating a small circle at B and draw the diameter CD, find the midpoint E of AD and join CE for another median, now we find F which is the centroid of the triangle ACD. That cuts the line in two third/one third, and so we use another circle with center F and radius FB to find the remaining point G. 

Level 18: Construct two new circles of radius AB where each pair of the three circles is tangent.

Hint: Let’s play pool?

Solution: The pool configuration is exactly what we will need to have the pairwise tangent. The rest is just construct it, nothing special with this level.

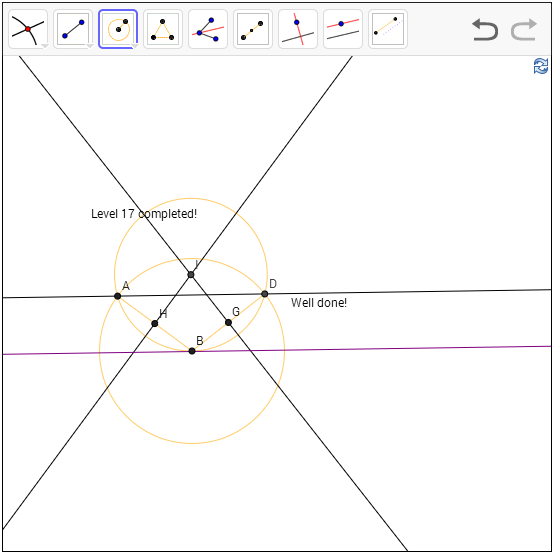
Level 17: Given a point A, a line, and a point B. Construct a circle that passes through A and is tangent to the line at B.

Hint: The circle passes through A and B, what else?

Solution: The circle must also pass through the mirror image of A. The line is a tangent, which means the line through B perpendicular to it is the diameter. The point D, the mirror image of A, can be constructed by first constructing a parallel line through A parallel to the tangent, and intersect it with the circle with center B and radius AB. The rest? It is just level-15, the circumcircle of A, B and D!

For economy we could have just constructed the perpendicular bisector of AB and then the line through B perpendicular to the tangent and use that as the circumcenter, but it would be hard to explain why that’s true.

Level 16: Given a line, a line segment CD, and a point O. Construct a circle with center O that cuts off a segment congruent to CD on the given line.

Hint: The same old hint – perpendicular bisector of chord pass through center.

Solution: The segment cuts off by the required circle is a chord, and the perpendicular bisector of the chord must pass through center. So let construct the perpendicular bisector by constructing the line pass through O perpendicular to the given segment. That gives us the point J. The point J bisect the chord, and the chord must have length CD, so just find the midpoint of CD (name it E), and then draw a circle with center J with length CE, that gives us the point K, the circle with center O and radius OK give us the solution.

Level 15: Construct the circumcircle of a triangle

Hint: All three sides are chord of the circumcircle, and the perpendicular bisector of chord …

Solution: … pass through center! Just construct two perpendicular bisectors of two sides, their intersection must be the center of the circumcircle. The radius? Just use any of A,B or C!