I hope you had fun with the game, just like I do, the answer provided here are meant to be a sample solution. There are, of course, other ways to accomplish the same goal. I am sure the answers are correct, but in case you think my answer is inaccurate or you have better solutions, please leave me comments!
Monday, June 23, 2014
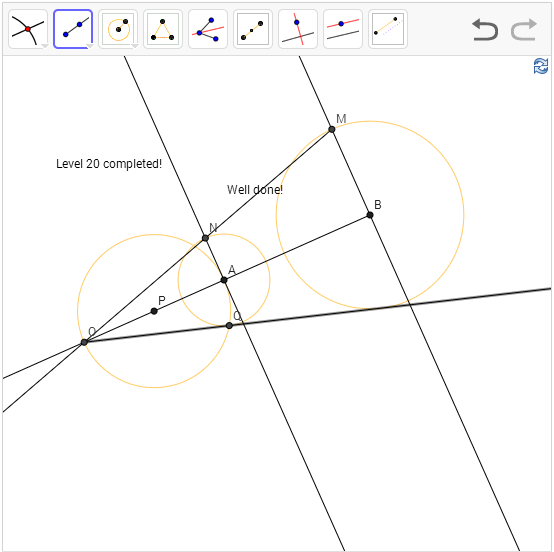
Level 20: Construct a line (segment) tangent to both circles. Construct the outer tangent line.
Hint: Think ratios.
Solution: First construct the ray AB, and
let the outer tangent line intersect AB at O. Now OA:OB should be (radius of A:
radius of B). To find such point O, we use the similar triangle NAO and MBO.
Once we found the point O, we need to find a point C on circle A such that OCA
is a right angle. Now we leverage another fact, angle subtended by the diameter
on a circle is the right angle, so we construct the midpoint P of O and A, draw
the circle with center P and radius PA, so the intersection between the circle
would give us the point C and we are done.
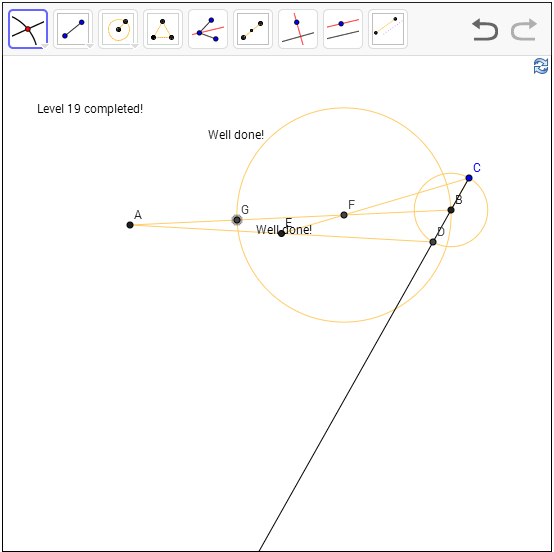
Level 19: Construct two points, such that the segment is cut into three equal pieces.
Hint: Perhaps unrelated – study the
centroid of a triangle.
Solution: The centroid of a triangle is
found by intersecting the median, the median is defined by the intersection
between the midpoint of an edge and the opposite vertex. The interesting thing
about this is that it can be shown that the intersection point always cut the
median into two-third on the vertex side and one third on the remaining side.
It is this property that we will leverage for this level.
With
that in mind, we make AB the median, which means A is the opposite vertex and B
is the midpoint of some base line, construct the base line by creating a small
circle at B and draw the diameter CD, find the midpoint E of AD and join CE for
another median, now we find F which is the centroid of the triangle ACD. That cuts
the line in two third/one third, and so we use another circle with center F and
radius FB to find the remaining point G.
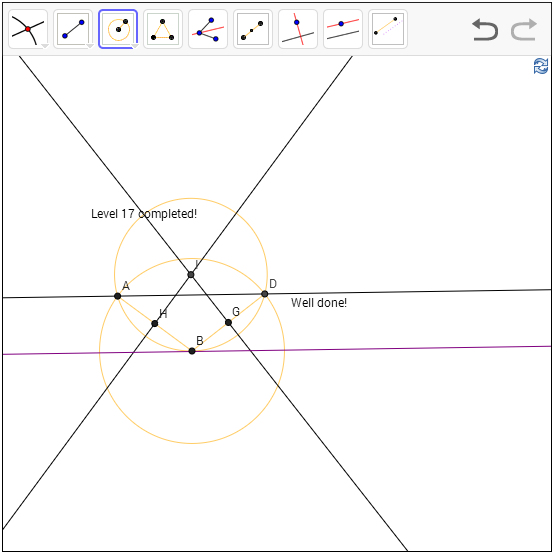
Level 17: Given a point A, a line, and a point B. Construct a circle that passes through A and is tangent to the line at B.
Hint: The circle passes through A and
B, what else?
Solution: The circle must also pass through
the mirror image of A. The line is a tangent, which means the line through B
perpendicular to it is the diameter. The point D, the mirror image of A, can be
constructed by first constructing a parallel line through A parallel to the
tangent, and intersect it with the circle with center B and radius AB. The
rest? It is just level-15, the circumcircle of A, B and D!
For
economy we could have just constructed the perpendicular bisector of AB and
then the line through B perpendicular to the tangent and use that as the
circumcenter, but it would be hard to explain why that’s true.
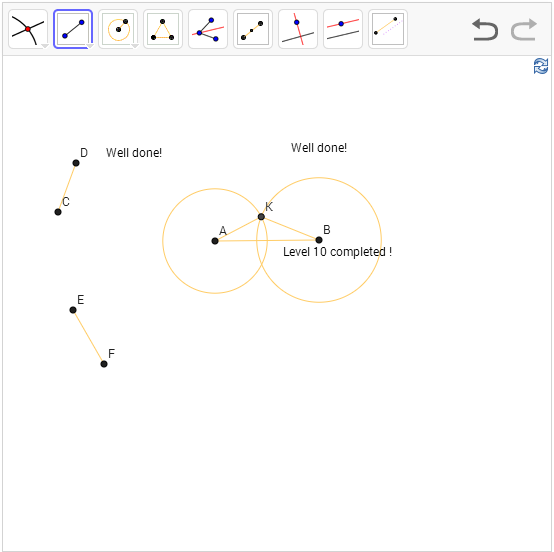
Level 16: Given a line, a line segment CD, and a point O. Construct a circle with center O that cuts off a segment congruent to CD on the given line.
Hint: The same
old hint – perpendicular bisector of chord pass through center.
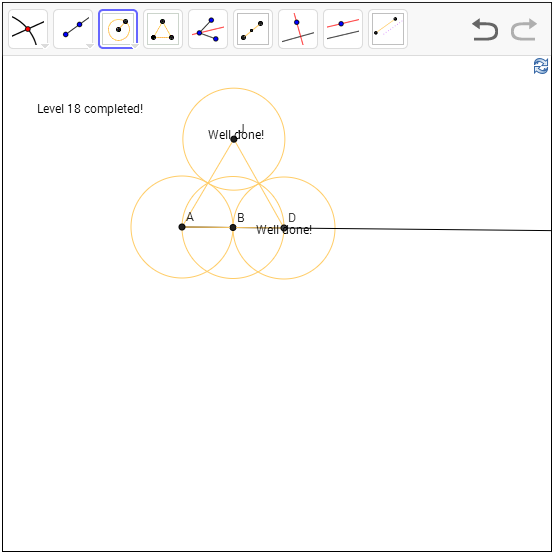
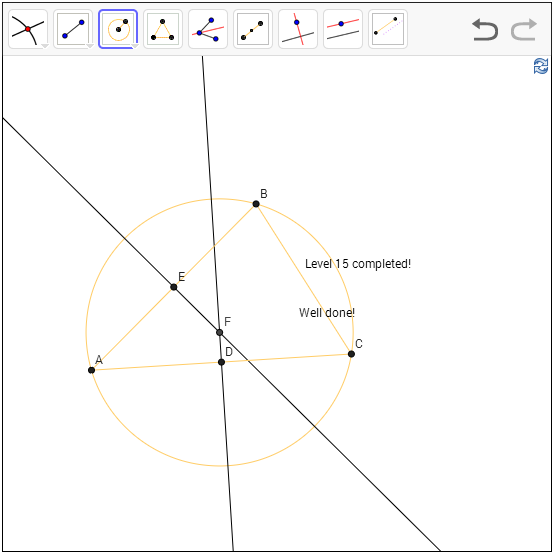
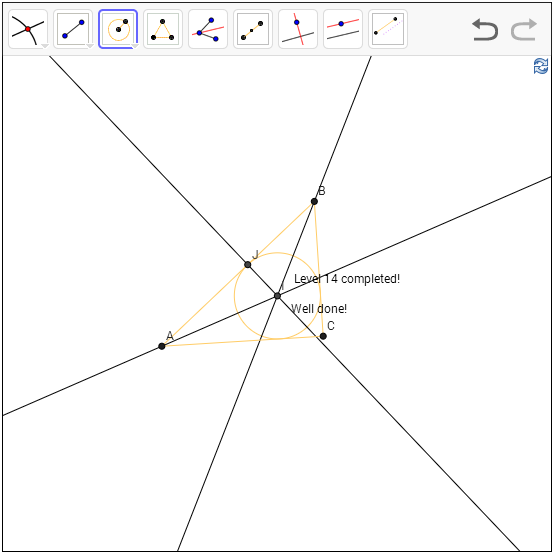
Level 14: Construct the in-circle of a triangle:
Hint: The center
of the in-circle must have same distance to the triangle lines. In particular,
two of the three lines?
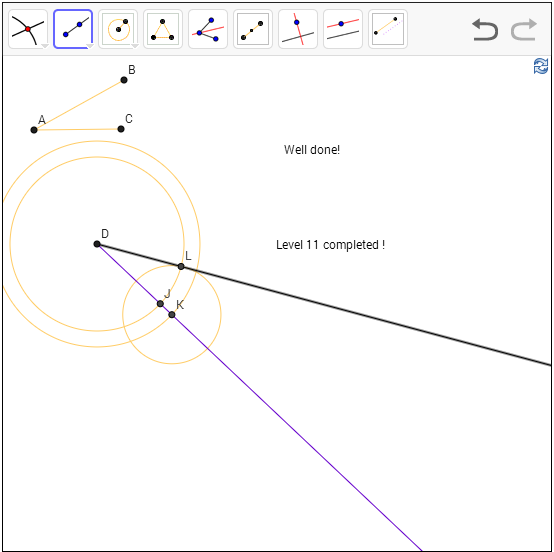
Level 11: Construct an angle on the given line equals to the given angle
Hint: Reproduce
triangle with specified length and base
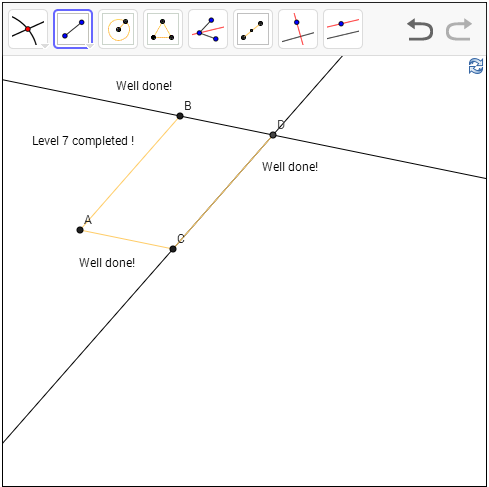
Level 7: Construct a line segment with the same length and same direction as line segment AB but with begin point C.
Hint: Think
parallelogram
Solution: Suppose
we have the required line CD, join BD, then ABDC must be a parallelogram. Using the parallel line tool
in level 6. We can easily construct this parallelogram by first constructing a
line at B parallel to AC, and then a line at C parallel to AB, the new
intersection point D is the parallelogram point.
Level 6: Construct a parallel line through point C
Hint: A line perpendicular
to a perpendicular line is parallel.
Solution: The
hint spell out the answer! First, construct a line through C perpendicular to
AB. Then construct a line through C perpendicular to the previous line, the
line must pass through C, and it must perpendicular to the line perpendicular
to AB, so it must be parallel to AB, so we are done.
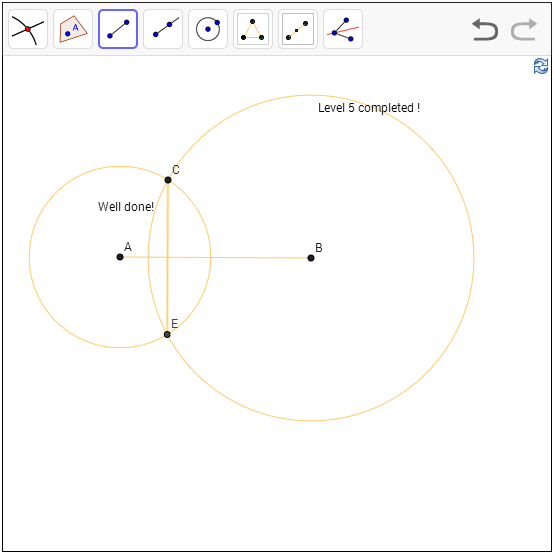
Level 5: Construct a line (segment) perpendicular to line segment AB going through point C.
Hint:
Perpendicular bisector of a chord go through the center.
Solution: Without
any particular reason, let construct two circles with center A and center B
with radius AC and BC respectively. The two circle intersect at C and we name
the other intersection E. Name the intersection between CE and AB as F. Now CF
= EF because of symmetry. Triangle BCF is congruent to triangle BEF, so angle
CFB = angle EFB, but they must also sum to 180 degree, so it is a right angle
and we are done.
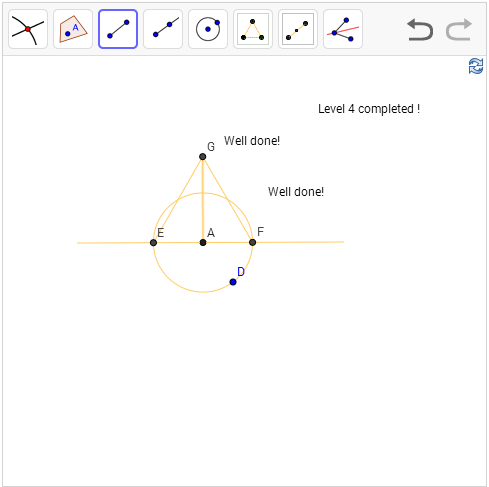
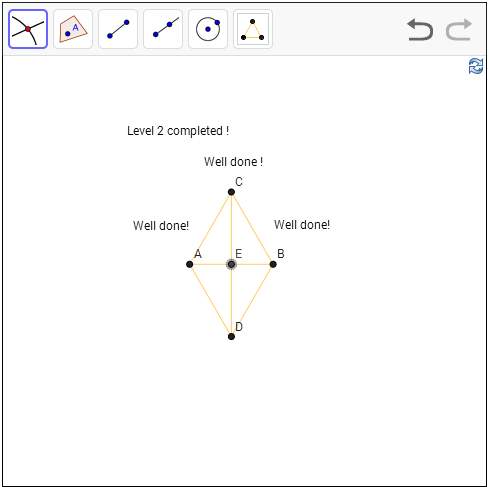
Level 4: Construct a line (segment) that goes through point A perpendicular to the given line segment
Hint: Make some
new point to unblock. Diagonal of rhombus are perpendicular to each other.
Solution: Given
the hint, all we need to do is do redo the rhombus trick in level 2. But there
is just one point? No worries, just create one using the point of the object
tool. We just pick point D somewhere, to make A the midpoint, I used the
circle tool to construct a circle with center A and radius AD. Mark the two intersections as E and F, and A is obviously the midpoint of EF. To complete the
construction, note that we already know A is the intersection point between the
diagonals, so we only need one equilateral triangle and join the vertex to A,
and we are done.
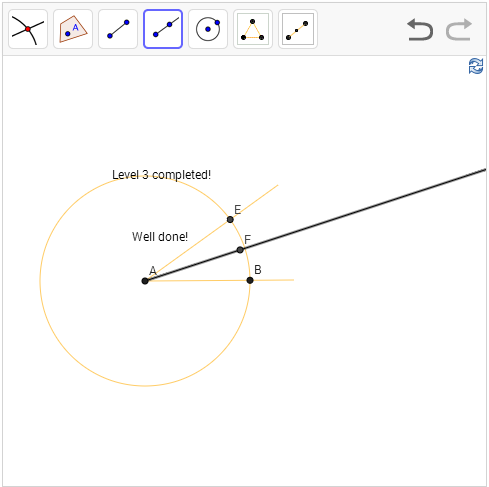
Level 3: Construct a line (segment) that bisects the given angle
Hint: The angle
bisector is an axis of symmetry.
Solution: It is
natural to construct a circle with center A and radius AB, the circle intersect
the other line at E. Now, imagine the angle bisector exists, it must be an axis
of symmetry that maps B to E. Therefore, the midpoint of E must lie of the
angle bisector, and we are done!
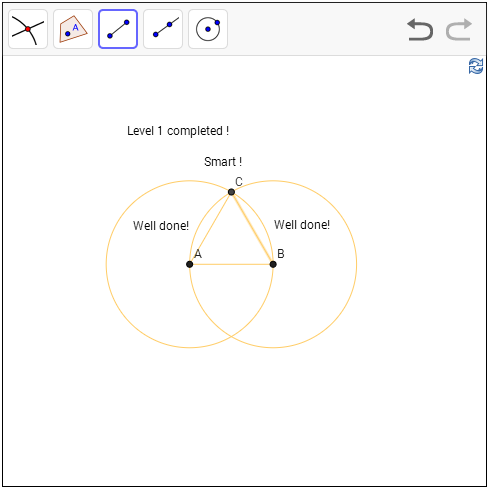
Level 1: Construct an equilateral triangle from the line segment AB.
Hint: You only
need another point C so that it is equal distance from A and from B.
Solution: This is
a very simple problem (after all this is just level 1) – the solution is as
follow – you construct the other vertex C of the equilateral triangle. The
point C must have AC = AB, so it must lie on the circle with center A and
radius AB. The point C must also have BA = BC, so it must lie on the circle
with center B and radius BA, therefore the solution is as follow
Euclid the game spoiler
This blog is written to show case the solutions for https://kasperpeulen.github.io/
Do NOT read this blog if you want to play the game for your
own, it was fun for me so I don’t want to spoil your fun. But if you are stuck,
or if you just want the solutions, here they are.
Subscribe to:
Posts
(
Atom
)